interview - coding patterns - breadth first search

src: Breadth First Search or BFS for a Graph - GeeksforGeeks

How Does the BFS Algorithm Work?

Starting from the root, all the nodes at a particular level are visited first and then the nodes of the next level are traversed till all the nodes are visited.

To do this a queue is used. All the adjacent unvisited nodes of the current level are pushed into the queue and the nodes of the current level are marked visited and popped from the queue.

Illustration:

Let us understand the working of the algorithm with the help of the following example.

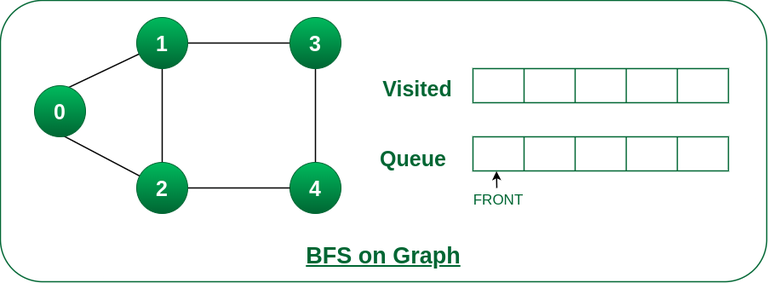
Step1: Initially queue and visited arrays are empty.

Queue and visited arrays are empty initially.

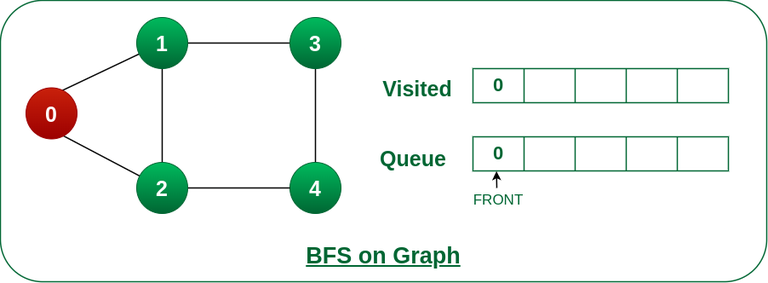
Step2: Push node 0 into queue and mark it visited.

Push node 0 into queue and mark it visited.

Step 3: Remove node 0 from the front of queue and visit the unvisited neighbours and push them into queue.

Remove node 0 from the front of queue and visited the unvisited neighbours and push into queue.

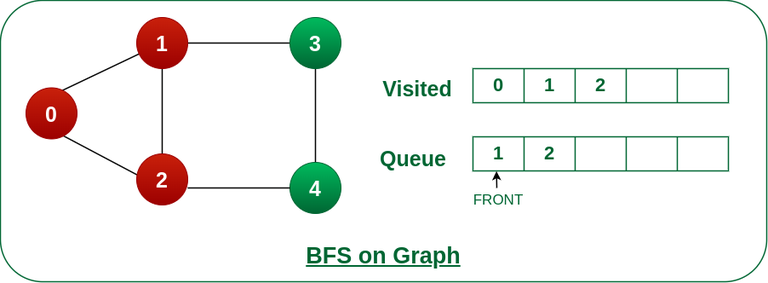
Step 4: Remove node 1 from the front of queue and visit the unvisited neighbours and push them into queue.

Remove node 1 from the front of queue and visited the unvisited neighbours and push

Step 5: Remove node 2 from the front of queue and visit the unvisited neighbours and push them into queue.

Remove node 2 from the front of queue and visit the unvisited neighbours and push them into queue.

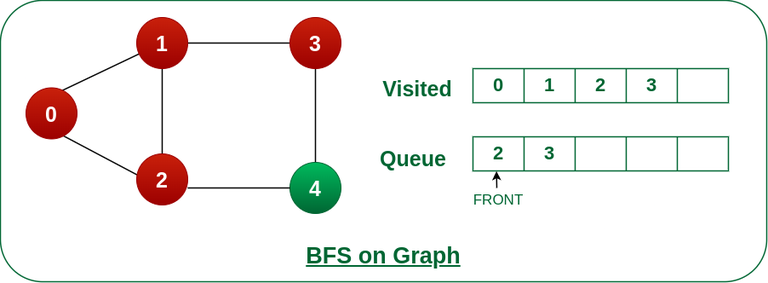
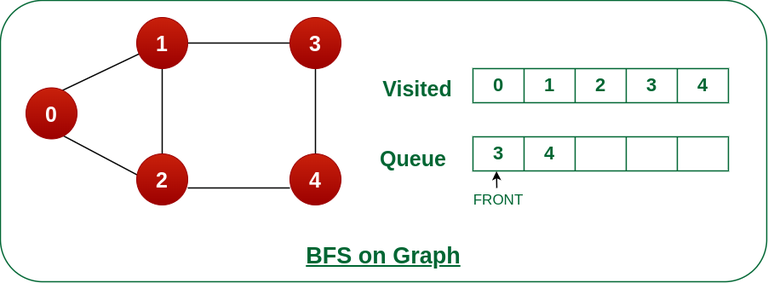
Step 6: Remove node 3 from the front of queue and visit the unvisited neighbours and push them into queue. 
As we can see that every neighbours of node 3 is visited, so move to the next node that are in the front of the queue.

Remove node 3 from the front of queue and visit the unvisited neighbours and push them into queue. 

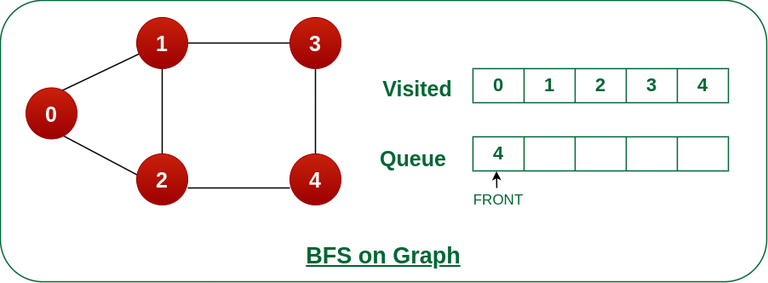
Steps 7: Remove node 4 from the front of queue and visit the unvisited neighbours and push them into queue. 
As we can see that every neighbours of node 4 are visited, so move to the next node that is in the front of the queue.

Remove node 4 from the front of queue and visit the unvisited neighbours and push them into queue.

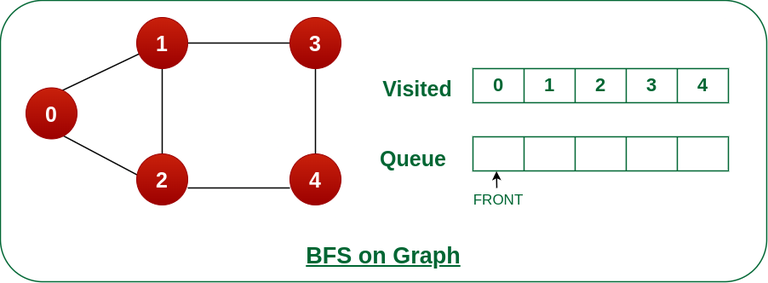
Now, Queue becomes empty, So, terminate these process of iteration.

Complexity Analysis of Breadth-First Search (BFS) Algorithm

V is the number of nodes and E is the number of edges.

Time Complexity of BFS Algorithm: O(V + E)

• BFS explores all the vertices and edges in the graph. In the worst case, it visits every vertex and edge once. Therefore, the time complexity of BFS is O(V + E), where V and E are the number of vertices and edges in the given graph.

Space Complexity of BFS Algorithm: O(V)

• BFS uses a queue to keep track of the vertices that need to be visited. In the worst case, the queue can contain all the vertices in the graph. Therefore, the space complexity of BFS is O(V), where V and E are the number of vertices and edges in the given graph.

Applications of BFS in Graphs

BFS has various applications in graph theory and computer science, including:

• Shortest Path Finding: BFS can be used to find the shortest path between two nodes in an unweighted graph. By keeping track of the parent of each node during the traversal, the shortest path can be reconstructed.
• Cycle Detection: BFS can be used to detect cycles in a graph. If a node is visited twice during the traversal, it indicates the presence of a cycle.
• Connected Components: BFS can be used to identify connected components in a graph. Each connected component is a set of nodes that can be reached from each other.
• Topological Sorting: BFS can be used to perform topological sorting on a directed acyclic graph (DAG). Topological sorting arranges the nodes in a linear order such that for any edge (u, v), u appears before v in the order.
• Level Order Traversal of Binary Trees: BFS can be used to perform a level order traversal of a binary tree. This traversal visits all nodes at the same level before moving to the next level.
• Network Routing: BFS can be used to find the shortest path between two nodes in a network, making it useful for routing data packets in network protocols.

How does Level Order Traversal work?

The main idea of level order traversal is to traverse all the nodes of a lower level before moving to any of the nodes of a higher level. This can be done in any of the following ways: 

• the naive one (finding the height of the tree and traversing each level and printing the nodes of that level)
• efficiently using a queue.

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}
 
public void traverseTree(TreeNode root) {
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
 
    while (!queue.isEmpty()) {
        TreeNode node = queue.poll();
 
        if (node.left != null) {
            levelQueue.add(node.left);
        }
        if (node.right != null) {
            levelQueue.add(node.right);
        }
    }
}