interview - coding patterns - depth first search

src: DFS traversal of a Tree - GeeksforGeeks

DFS (Depth-first search) is a technique used for traversing trees or graphs. Here backtracking is used for traversal. In this traversal first, the deepest node is visited and then backtracks to its parent node if no sibling of that node exists

DFS Traversal of a Graph vs Tree:

In the graph, there might be cycles and disconnectivity. Unlike the graph, the tree does not contain a cycle and are always connected. So DFS of a tree is relatively easier. We can simply begin from a node, then traverse its adjacent (or children) without caring about cycles. And if we begin from a single node (root), and traverse this way, it is guaranteed that we traverse the whole tree as there is no dis-connectivity,

Examples:

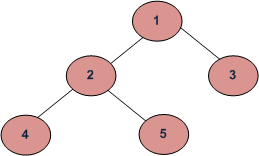
Input Tree:

Therefore, the Depth First Traversals of this Tree will be:

1. Inorder: 4 2 5 1 3
2. Preorder: 1 2 4 5 3
3. Postorder: 4 5 2 3 1

1. Inorder Traversal

Follow the below steps to solve the problem:

• Traverse the left subtree, i.e., call Inorder(left-subtree)
• Visit the root
• Traverse the right subtree, i.e., call Inorder(right-subtree)

Time Complexity: O(N)
Auxiliary Space: O(log N)

Uses of Inorder traversal

In the case of binary search trees (BST), Inorder traversal gives nodes in non-decreasing order. To get nodes of BST in non-increasing order, a variation of Inorder traversal where Inorder traversal is reversed can be used

2. Preorder Traversal

Follow the below steps to solve the problem:

• Visit the root
• Traverse the left subtree, i.e., call Preorder(left-subtree)
• Traverse the right subtree, i.e., call Preorder(right-subtree)

Time Complexity: O(N)
Auxiliary Space: O(log N)

Uses of Preorder

Preorder traversal is used to create a copy of the tree. Preorder traversal is also used to get prefix expressions of an expression tree.

3. Postorder Traversal

Follow the below steps to solve the problem:

• Traverse the left subtree, i.e., call Postorder(left-subtree)
• Traverse the right subtree, i.e., call Postorder(right-subtree)
• Visit the root

Time Complexity: O(N)
Auxiliary Space: O(log N)

Uses of Postorder

Postorder traversal is used to delete the tree. Please see the question for the deletion of the tree for details. Postorder traversal is also useful to get the postfix expression of an expression tree